Zur Berechnung der Wärmeleitung inhomogener Materialien über die Finite-Difference-Methode bietet dieser Artikel einen einfachen Einstieg mit Programmcode in Python. Als numerische Approximation bildet die Finite-Difference-Methode komplexe Bauteile in einem Netzwerk kleiner Umgebungen aus jeweils homogenen Bestandteilen ab, ohne dass aufwendige mathematische Ansätze erforderlich sind. Ein Anwendungsbeispiel aus der Bauwirtschaft wäre die Berechnung von Wärmebrücken, wie sie an den Übergängen von Baugruppen auftreten. Weil beim Neubau die Einhaltung strenger Normen der Energieeffizienz ohne eine detaillierte Beurteilung typischer Schwachstellen kaum mehr nachzuweisen ist, haben geeignete numerische Verfahren heute einen hohen Stellenwert.
Zweck dieser Abhandlung ist es zu zeigen, wie aus vereinfachenden Modellierungen einer Vielzahl kleiner Umgebungen gute Näherungen realer Bauteile entstehen. Auch möchte sie Gebäudeenergieberatern ein besseres Verständnis der Berechnung und Beurteilung von Wärmebrücken vermitteln.
Das zugehörige Python-Projekt steht mit allen Berechnungen auf GitHub zum Download bereit.
Sampling einer inhomogenen Struktur im Finite-Difference-Grid
Die Modellierung realer, inhomogener Bauteile im Finite-Difference-Grid beginnt mit dem Sampling der Wärmeleitfähigkeit des Materials an den Knotenpunkten eines Gitters.
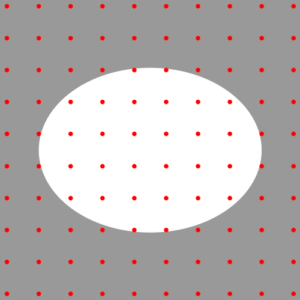
Das Sampling setzt die Werte an Knotenpunkten für die gesamte Fläche von Quadraten mit Kantenlängen in Größe des Abtastrasters an. Bei diesem Vorgang fällt ein Sampling-Error an, der Details der Originalstruktur verloren gehen läßt. Deswegen werden Ergebnisse von Berechnungen mit der Finite-Difference-Methode umso genauer werden, je kleiner das Abtastraster. Weil jedoch mit der Zahl der Knotenpunkte der Rechenaufwand steigt, gilt es, hier ein Optimum zu finden.

Abbildung 2 zeigt die modellierte Struktur, welche die auch von Digitalbildern bekannte Pixelung aufweist. Obwohl die Darstellung fürs Auge recht grob aussieht, würde eine Finite-Difference-Abschätzung der Wärmeleitung auf dieser Grundlage bereits brauchbare Ergebnisse liefern.
Berechnung der Temperatur von Knotenpunten
Zur Berechnung der Knotentemperaturen gelten folgende Randbedingungen der Modellierung von Wärmebrücken:
- In den Knoten wird keine Wärme erzeugt, wie etwa durch chemische Reaktion beim Aushärten von Zement.
- Es hat sich ein stationärer Zustand eingestellt, in dem also die Temperatur keiner zeitlichen Änderung unterliegt. Dazu müssen Innen- und Außentemperatur von Gebäuden über einen längeren Zeitraum unverändert bleiben, damit sich alle Bauteile entsprechend aufwärmen.
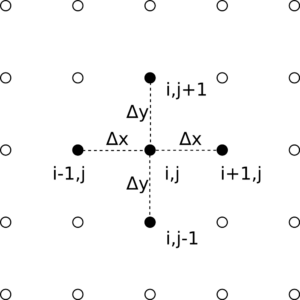
Unter den genannten Randbedingungen wird die Temperatur eines Knotens (i,j) ausschließlich von den Temperaturen der umliegenden Knoten bestimmt, hier also (i-1,j), (i+1,j), (i,j-1) und (i,j+1). Weitere Annahmen der Modellierung sind gleiche Knotenabstände Δx=Δy in der Horizontalen und Vertikalen, sowie ein vernachlässigbarer Einfluss von den Diagonalen.
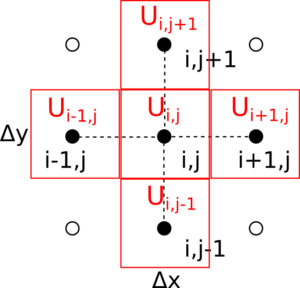
Mit konstanten Wärmeleitfähigkeiten in Quadranten der Kantenlänge Δx=Δy um Knotenpunkte entsprechen die fünf Werte Ui-1,j, Ui,j, Ui+1,j, Ui,j+1 und Ui,j-1 den Samples der Diskretisierung wie aus Abbildung 2.
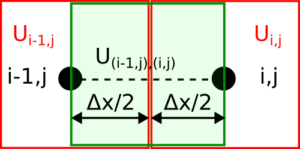
Um nun den Wärmefluss zwischen Knoten (i-1,j) und (i,j) zu berechnen, fehlt noch der Wert für die in Abbildung 5 grün unterlegte Wärmebrücke mit Leitfähigkeit U(i-1,j),(i,j). Diese setzt sich aus zwei jeweils homogenen Hälften einer Breite Δx/2 mit Wärmeleitfähigkeiten Ui-1,j und Ui,j zusammen. In der Energieberatern wohlbekannten Weise addieren sich hier die Wärmedurchgangswiderstände der beiden Hälften.
R_{(i-1,j),(i,j)} = \frac{1}{2U_{i-1,j}} + \frac{1}{2U_{i,j}}Mithin ergibt sich die Leitfähigkeit U(i-1,j),(i,j) als:
U_{(i-1,j),(i,j)} = \frac{1}{ \frac{1}{2U_{i-1,j}} + \frac{1}{2U_{i,j}}}und ausmultipliziert:
\begin{align}
U_{(i-1,j),(i,j)} = 2\frac{U_{i-1,j}U_{i,j}}{U_{i-1,j}+U_{i,j}}
\end{align}Der Wärmefluss q(i-1,j),(i,j) von Knoten (i-1,j) zu (i,j) ergibt sich mit den Temperaturen Ti-1,j und Ti,j als:
\begin{align}
q_{(i-1,j),(i,j)} = U_{(i-1,j),(i,j)}(T_{i-1,j} - T_{i,j})
\end{align}Unter den Randbedingungen keiner Wärmeerzeugung in Knotenpunkten und des stationären Zustands müssen sich nun die Wärmeströme aufheben, die in Knoten hinein und hinaus fließen. Es gilt also:
\begin{aligned}
& q_{(i-1,j),(i,j)}\\
&+ \space q_{(i,j),(i+1,j)}\\
&+ \space q_{(i,j-1),(i,j)}\\
&+ \space q_{(i,j),(i,j+1)} = 0
\end{aligned}Abgesehen von der etwas unhandlichen Notation der Knotenindizes haben wir damit eine einfache Gleichung, welche die Temperatur jedes Knotenpunkts aus denen der umliegenden Knoten, gewichtet mit der jeweiligen Wärmeleitfähigkeit, ermittelt. Wie versprochen, sind hierzu keine fortgeschrittenen mathematischen Kenntnisse vonnöten.
Vereinfachte Schreibweise der Knotengleichungen
Zum besseren Verständnis bietet sich eine vereinfachte Schreibweise der Knotengleichungen an. Statt der Indizes (i-1,j), (i,j), (i,j-1) und (i,j+1) bezeichnen l (left), r (right), b (bottom) und t (top) nun die Nachbarn des Knotens (i,j). Die Summe der Wärmeströme schreibt sich dann wie folgt:
\begin{aligned}
& q_{l,(i,j)}\\
&+ \space q_{(i,j),r}\\
&+ \space q_{b,(i,j)}\\
&+ \space q_{(i,j),t} = 0
\end{aligned}Unter Auslassung des Knotenindexes (i,j) erhält man also für die Wärmeströme:
\begin{align}
q_l + q_r + q_b + q_t = 0
\end{align}Unter Verwendung der gleichen l,r,b,t Indizierung für Wärmeleitfähigkeiten und Temperaturen sowie c (center) der Temperatur im Mittelpunkt:
\begin{aligned}
&U_l(T_l - T_c)\\
&+ U_r(T_r - T_c)\\
&+ U_b(T_b - T_c)\\
&+ U_t(T_t - T_c) = 0
\end{aligned}oder umgestellt
U_lT_l + U_rT_r + U_bT_b + U_tT_t\\ - (U_l + U_r + U_b + U_t)T_c = 0
Mit
\Sigma_U = U_l + U_r + U_b + U_t
ergibt sich schließlich die Schreibweise für das System der Knotengleichungen des nächsten Abschnitts:
U_lT_l + U_rT_r + U_bT_b + U_tT_t\\ - \Sigma_UT_c = 0
Aufstellen eines linearen Systems von Knotengleichungen
Wärmeflüsse entstehen durch Temperaturgefälle, wie beispielsweise zwischen beheizten Innenräumen und der Außenluft. Abhängig von der Wärmeleitfähigkeit verlaufen diese ungleichmäßig, was sich in Temperaturdifferenzen zwischen Knotenpunkten der Finite-Differenz-Modellierung widerspiegelt. Demzufolge gilt es, die Temperaturen sämtlicher Knotenpunkte in einem linearen Gleichungssystem zu berechnen, um den Wärmefluss insgesamt und mithin ein Maß für die Leitfähigkeit zu erhalten.
Wie im vorangehenden Abschnitt gezeigt, erhält man in jedem Knoten des Finite-Difference-Grids eine Gleichung, welche die Knotentemperatur Tc aus den Temperaturen Tl, Tr, Tb und Tt sowie aus dem Sampling bekannten Wärmeleitfaktoren ermittelt. Die Knotentemperaturen ergeben sich also aus jeweils vier unbekannten anderen Knotentemperaturen. Daraus erhalten wir ein System mit unbekannten Variablen entsprechend der Zahl der Knotenpunkte, und ebenso vielen Gleichungen. Was bei tausenden von Variablen unlösbar erscheinen mag, ist im Zeitalter fortgeschrittener numerischer Entwicklungsumgebungen mit ihren Algorithmen eine leichte Übung! Dies erfordert allerdings Gleichungen in Matrixnotation. Falls von Interesse, findet sich hierzu eine kurze Einführung in Anhang 1.
Das nachfolgend beschriebene Verfahren baut auf Kyle Niemeyers [3] zur weiterführenden Lektüre sehr zu empfehlenden Abhandlung zur Lösung elliptischer PDEs auf. Hier sind fortgeschrittene Ansätze für lineare Gleichungssysteme mit einer großen Zahl von Variablen erläutert.
Eingangsvariablen der Berechnung sind die Matrix C mit entsprechend des Abschnitts zum Sampling eingelesenen Wärmeleitwerten, sowie als Randbedingungen die Temperaturen des Innenraums und der Außenluft. Hieraus folgt ein Gleichungssystem mit den Vektoren der Knotentemperaturen u und Ergebnissen der Gleichungen b:
Au = b
Bei einer Struktur von (m x n) Abtastwerten des Materials haben die Matrix A und Vektoren u, b eine Dimension von (m * n, m * n) beziehungsweise (m * n). Anders gesagt ist die Matrix A quadratisch mit einer Kantenlänge entsprechend der Zahl der Bildpunkte beziehungsweise Abtastwerte. Nehmen wir als Minimalbeispiel eine Matrix C mit (3 x 3) Werten:
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\
U_t & 0 & 0 & -\Sigma_U & U_r & 0 & U_b & 0 & 0\\
0 & U_t & 0 & U_l & -\Sigma_U & U_r & 0 & U_b & 0 \\
0 & 0 & U_t & 0 & U_l & -\Sigma_U & 0 & 0 & U_b \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\\
\end{bmatrix}
\begin{bmatrix}
T_{1,1}\\
T_{1,2}\\
T_{1,3}\\
T_{2,1}\\
T_{2,2}\\
T_{2,3}\\
T_{3,1}\\
T_{3,2}\\
T_{3,3}
\end{bmatrix}
=
\begin{bmatrix}
T_i\\
T_i\\
T_i\\
0\\
0\\
0\\
T_o\\
T_o\\
T_o
\end{bmatrix}Hier wurde an der Oberseite des Materials (erste Reihe der Matrix C) eine Innentemperatur Ti angesetzt und an der Unterseite (letzte Reihe der Matrix) eine Außentemperatur To. Man beachte die tridiagonale Struktur der Matrix A, wie auch die zu Null gesetzten Faktoren an den linken und rechten Rändern des Bauteils. Das Bauteil wird also so behandelt, als wäre es zu den Seiten perfekt von der Umgebung isoliert. Das mag nicht der Realität entsprechen, erleichtert aber die Programmierung, weil sich ansonsten die Frage stellen würde, welche Wärmeleitwerte man fürs Unbekannte setzen sollte. Eine programmtechnische Ausführung ist in der Funktion fill_system_weights(C) zu finden.
Die fehlenden Temperaturen T2,1, T2,2 und T2,3 können nun mithilfe der inversen Matrix A berechnet werden:
u = A^{-1}bDas programmierte Minimalbeispiel befindet sich hier.
Finite-Difference Anwendungsbeispiele
Nun zwei Beispiele zur Modellierung von Aufgabenstellungen der Gebäudeenergieeffizienz, wo bei Außenwänden die Wärmedurchgangswiderstände angrenzender Luftschichten eingehen. Weil diese nur über ihre Wärmeleitfähigkeit, nicht jedoch ihre räumlichen Abmessungen definiert sind, bedarf es zum Übertrag in ein Finite-Difference-Grid einer speziellen Skalierung.
Zunächst wird zur Überprüfung der hergeleiteten Gleichungen und des Programmcodes die Approximation einer Wand aus homogenen Schichten mit theoretischen Werten verglichen. Es folgt die Modellierung einer Wand aus Hochlochziegel zur Wärmeleitung inhomogener Strukturen über das hier entwickelte Finite-Difference-System.
Homogene Wand
Als erstes Beispiel die Finite-Difference-Modellierung einer horizontal wie vertikal homogenen Wand aus mehreren Schichten. Weil das Temperaturgefälle dieser Konstellation mithilfe von analytischen Formeln berechnet werden kann, erfolgt zur Funktionskontrolle ein Vergleich der theoretischen und approximierten Werte. Der zugehörige Programmcode demonstriert auch die Skalierung des Finite-Difference-Grids auf die Abmessungen realer Bauteile.
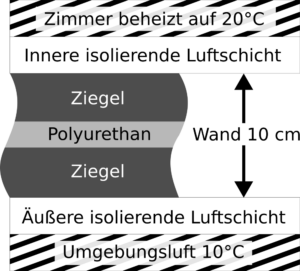
Die Modellwand des Beispiels besteht aus zwei Schichten Ziegelstein einer Dicke von 4 cm, sowie einer 2cm Dämmschicht aus Polyurethan. Isolierende innere und äußere Luftschichten gemäß ISO 6946:2017 grenzen an die Innen- und Außenseiten der Wand und gehen in die Berechnung des Wärmedurchgangskoeffizienten ein.
Den theoretischen Wert des Wärmedurchgangskoeffizienten Uw der Wand erhält man mit dem Kehrwert der Summe der Einzelwiderstände der Schichten:
U_w = \frac {1}{R_{se} + R_{z1} + R_p + R_{z2} + R_{si}}Hier stehen Rsi und Rse für die Wärmedurchgangswiderstände von Innen- und Außenluft nach ISO 6946, Rz1 und Rz2 für die Wärmedurchgangswiderstände der Ziegelschichten und Rp für den des Polyurethans. Für Innen- und Außenluft sind die Wärmedurchgangswiderstände unabhängig von der Dicke der Luftschichten mit 0,13 beziehungsweise 0,04 m2K/W vorgegeben. Weiterhin gelten für diese Berechnung Wärmeleitfähigkeiten von 0,62 W/m2K für Ziegelstein sowie 0,028 W/m2K für Polyurethan. Mit Schichtdicken von 4 cm ergeben sich dann Rz1 und Rz2 als 0,06452 m2K/W. Für die 2 cm Polyurethan erhält man Rp = 0,7143 m2K/W. Damit ist der theoretische Wert des Wärmedurchgangskoeffizienten der Wand Uw = 0,987 W/m2K.
Uw = 1 / (0.13 + 0.04 + 2 * 0.06452 + 0.7143) = 0.987Zur Aufstellung des Finite-Difference-Grids einer numerischen Approximation stellt sich jedoch die Frage, wie die isolierenden Luftschichten nach ISO 6946 in diskrete Schritte abzubilden sind. Eine Möglichkeit ist, Zimmer- und Außenluft sowie die isolierenden Luftschichten getrennt zu behandeln. Die schraffierten Bereiche aus Abbildung 6 für Zimmer- und Außenluft bekommen dann die Breite einer Schrittweite im Grid, mit fester Temperatur und unbegrenzter Wärmeleitfähigkeit. Die Wärmedurchgangskoeffizienten der Luftschichten von ebenfalls einer Schrittweite sind dann so zu bemessen, dass sich entsprechend der Dicke die Wärmedurchgangswiderstände nach ISO 6946 ergeben.
Bei einer Finite-Difference-Schrittweite von 1 cm entfallen also 10 Schritte auf die Wand. Die isolierenden Luftschichten sowie die Innen- und Außenluft passen wie dargelegt jeweils in eine Schrittweite. Insgesamt benötigt somit das numerische Modell in der Vertikalen 14 Schritte.
Die Skalierung des Modells erfolgt nun, indem passende Werte der Wärmeleitfähigkeiten der ISO 6946 Luftschichten eingesetzt werden. Weil diese Dicken von je 1 cm haben, ist ein Skalierungsfaktor von 0,01 anzusetzen. Dann sind Use=0.25 W/mK und Usi=0.07692 W/mK.
Use = 1 / Rse * 0.01 = 1 / 0.04 * 0.01 = 0.25
Usi = 1 / Rsi * 0.01 = 1 / 0.13 * 0.01 = 0.07692Die Finite-Difference-Approximation des Wärmedurchgangskoeffizienten der Wand erhält man schließlich über den durchschnittlichen Temperaturabfall in einer der isolierenden Luftschichten. Im Programm nimmt man einfach den Mittelwert der zweiten Zeile der Temperaturmatrix und kommt über einen Dreisatz zum Gesamtwiderstand der Konstellation.
# to get the wall's heat conductivity from the approximation, first compute
# the average temperature drop across the inner layer of insulating air
# since the computed values represent the middle of air layers, the temperature
# drop needs be doubled.
delta_t_i = (T_i - np.mean(u_square[1,:])) * 2
R_approx_total = R_si * (T_i - T_o)/delta_t_i
Siehe hierzu die Textausgabe des Demonstrationsprogramms:
Result matrix of temperatures:
[[20. 20. ]
[19.35854291 19.35854291]
[18.63750057 18.63750057]
[18.47833007 18.47833007]
[18.31915958 18.31915958]
[18.15998909 18.15998909]
[16.31815908 16.31815908]
[12.79366956 12.79366956]
[10.95183956 10.95183956]
[10.79266906 10.79266906]
[10.63349857 10.63349857]
[10.47432807 10.47432807]
[10.19737141 10.19737141]
[10. 10. ]]
Simulated/theortical inner air layer temperature drop: 1.283/1.283
Simulated/theortical outer air layer temperature drop: 0.395/0.395
simulated/theoretical temperature drop across polyurethane: 7.049/7.049
simulated/theoretical brick layers with pur insulation 10 cm coefficient of heat conductivity:
U [W/(m² K)] = 0.987/0.987Wie zu zeigen war, gleichen sich theoretische und numerisch approximierte Ergebnisse exakt. Dies gelingt, weil in diesem einfachen Fall das Finite-Difference-Grid das Material ohne Abweichungen abbildet.
Das Beispiel unterstreicht den Stellenwert einer effektiven Dämmschicht zur Errichtung energieeffizienter Gebäude. Die 10 cm dünne Wand mit nur 2 cm Polyurethan erreicht eine bessere Dämmung als 28 cm dicke, aus Hochlochziegel gemauerte Wände. 70 % des Temperaturgefälles des Beispiels liegen innerhalb der 2 cm Polyurethan!
Modellierung einer inhomogenen Wand aus Hochlochziegel
Nachdem das vorhergehende Beispiel der Verifikation der numerischen Approximation diente, nun das Modell einer realen Wand aus einem selten verbauten Hochlochziegel.

Zur Berechnung realer Bauteile, in Ermangelung einer fortgeschrittenen Modellierungssoftware, besteht die erste Herausforderung in der Entwicklung einer schematischen Darstellung. Die untenstehende entstammt der kostenlosen Vektorgrafik Inkscape.
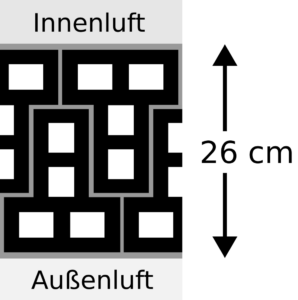
Für eine minimalistische Modellierung inhomogener Strukturen kann man nun ein Bitmap (ohne die Beschriftungen aus Abbildung 8) exportieren und in eine Matrix mit den Wärmeleitfähigkeiten des Finite-Difference-Grid umwandeln. In Inkscape sollte man dazu die Antialias-Einstellung auf 0 setzen, um keine unerwünschten Zwischentöne zu erhalten. All diese Schritte sind im dennoch recht kurzen Beispielprogramm png_model_2d implementiert.
| Material | Wärmeleitfähigkeit λ [W/(mK)] |
|---|---|
| Ziegelstein | 0,68 |
| Mörtel und Putz | 1,0 |
| Luft | 0,02614 |
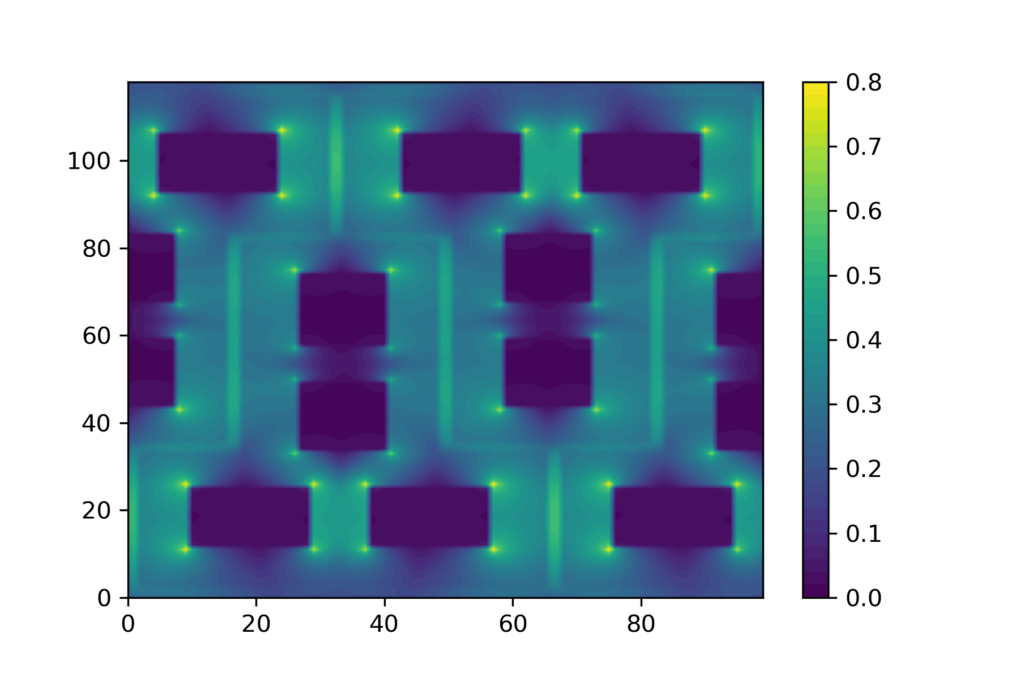
Zu den Wärmeleitfähigkeiten aus Tabelle 1 kommen noch die Wärmedurchgangswiderstände Rsi und Rse nach ISO 6946. Damit sind alle Materialien des Querschnitts definiert und man erhält man eine Matrix C sowie ein Gleichungssystem analog zum Abschnitt der Knotengleichungen. Mit den vom Algorithmus berechneten Temperaturen ergeben sich Magnituden der Wärmeflüsse wie in Abbildung 9. Je heller der Farbton, desto stärker der Wärmefluss mit klar erkennbaren Wärmebrücken entlang des Mörtels und rund um Luftlöcher.
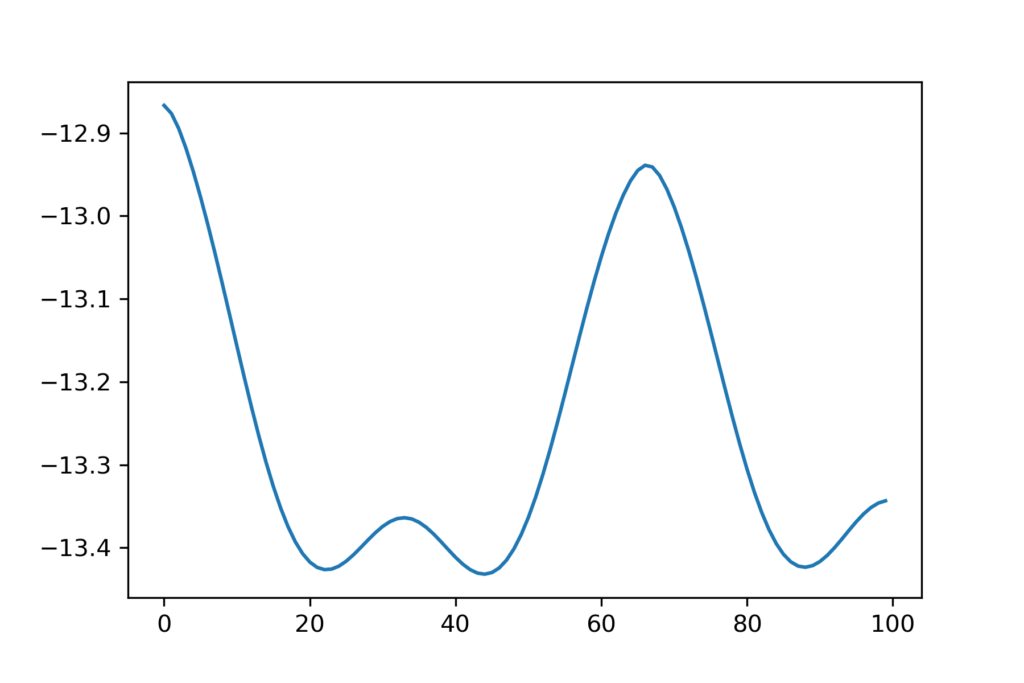
Auch die Temperaturen der Oberflächen der Wände zählen zu den Ergebnissen der Finite-Difference-Approximation. Unter der Randbedingung einer Innentemperatur von 20°C und Außentemperatur von -15°C weist die Außenseite der Wand Temperaturschwankungen entsprechend Abbildung 10 auf. Klar zu erkennen ist, wie oberhalb der Luftlöcher weniger Wärme übertragen wird, was sich in den dort kälteren Mauerbereichen widerspiegelt.
Zum Schluss noch der errechnete Wärmedurchgangskoeffizient der Wand. Dieser ergibt sich wie im vorhergehenden Abschnitt aus dem Temperaturabfalls entlang eines Querschnitts. Im Modell erreicht die rund 26 cm dicke Wand einen Wärmedurchgangskoeffizienten von 1,245 W/(m2K). Möglicherweise müsste man den Wert wegen konvektiver Effekte in den Luftlöchern noch nach oben korrigieren. Selbst die vorher untersuchte 10 cm dünne Wand erreichte wegen der 2 cm starken Dämmschicht aus Polyurethan mit 0,987 W/(m2K) einen deutlich besseren Wert! Luftlöcher in Ziegeln sind also kein Ersatz für moderne Dämmtechnik.
Anhang 1: Lineare Gleichungssysteme algorithmisch lösen
Zum Verständnis der algorithmischen Lösung linearer Systeme, wie in einer Finite-Difference-Aufgabenstellung, ein Gleichungssystem für Einsteiger:
\begin{aligned}
x + 2 y &= 0\\
2x - 3 y &= 1
\end{aligned}Für ein System mit zwei Variablen und zwei Gleichungen wird es genau eine Lösung geben. Diese ermittelt man beispielsweise durch eine Substitution:
\begin{aligned}
&x = -2y\\
&\space \Rightarrow\\
&2(-2y) - 3y = 1\\
&\space \Rightarrow\\
&y = -\frac{1}{7}\\
&x = -2(-\frac{1}{7}) = \frac{2}{7}
\end{aligned}So weit, so gut, nur lässt sich das furchtbar schlecht programmieren. In Matrizenschreibweise ist das Problem hingegen gut zu formalisieren. Wer mit der Schreibweise nicht vertraut ist, vergleiche das nachfolgende System mit dem eingangs angeführten „Gleichungssystem für Einsteiger“. Beide Darstellungen sind gleichwertig.
\begin{bmatrix}
1 & 2\\
2 & -3
\end{bmatrix}
\begin{bmatrix}
x\\
y
\end{bmatrix} =
\begin{bmatrix}
0\\
1
\end{bmatrix}Matrizen sind lineare Abbildungen und haben ihre Inverse als Umkehrfunktion. Es gilt folgender Zusammenhang, mit A als Matrix und b und c als Vektoren:
\begin{aligned}
A b &= c\\
A^{-1}Ab &= A^{-1}c\\
b &= A^{-1}c
\end{aligned}Weil eine Matrix multipliziert mit ihrer Inversen Werte auf sich selbst abbildet, können Gleichungssysteme durch beidseitiges Anwenden der Inversen aufgelöst werden.
Probe aufs Exempel:
\begin{aligned}
A &=
\begin{bmatrix}
1 & 2\\
2 & -3
\end{bmatrix}\\
A^{-1} &=
\begin{bmatrix}
0.42857143 & 0.285714291\\
0.28571429 & -0.14285714
\end{bmatrix}\\
A^{-1}A &=
\begin{bmatrix}
1 & 0\\
0 & 1
\end{bmatrix}\\
c &=
\begin{bmatrix}
0\\
1
\end{bmatrix}\\
b &= A^{-1}c
\\
b &=
\begin{bmatrix}
0.42857143 & 0.285714291\\
0.28571429 & -0.14285714
\end{bmatrix}
\begin{bmatrix}
0\\
1
\end{bmatrix}\\
b &=
\begin{bmatrix}
0.28571429\\
-0.14285714
\end{bmatrix}
=
\begin{bmatrix}
\frac{2}{7}\\
\frac{-1}{7}
\end{bmatrix}
\end{aligned}In Python:
A = np.array([[1,2],[2,-3]])
In [97]: A
Out[97]:
array([[ 1, 2],
[ 2, -3]])
A2 = np.linalg.inv(A)
In [106]: A2
Out[106]:
array([[ 0.42857143, 0.28571429],
[ 0.28571429, -0.14285714]])
In [102]: np.matmul(A, A2)
Out[102]:
array([[1., 0.],
[0., 1.]])
In [104]: np.matmul(A2,b)
Out[104]: array([ 0.28571429, -0.14285714])Lineare Gleichungssysteme in Matrixnotation erleichtern also die Auflösung von Systemen auch mit sehr vielen Unbekannten und die dazu gehörigen Algorithmen sind Bestandteil gebräuchlicher numerischer Umgebungen.
Anhang 2: Herleitung der Finite-Difference Knotengleichungen
Zahlreiche Quellen leiten die Knotengleichungen eines Finite-Difference-Systems für Wärmeleitung her, ohne jedoch eine leicht zugängliche Behandlung inhomogener Materialien zu liefern. Vielleicht ist diese Erweiterung zu naheliegend, um sich für wissenschaftliche Publikationen zu qualifizieren. Oder die Notation der Gleichungen würde sonst zu umständlich. Auch ist die in den Abschnitt der Knotenpunkte eingegangene Nullsumme der Wärmeströme so unmittelbar einleuchtend, dass es eigentlich keiner Herleitung bedarf.
Dennoch kurz ein Verweis auf die 1822 von Joseph Fourier [4] veröffentlichen Wärmegleichungen, die sehr gut im frei verfügbaren Lehrbuch zur Wärmeleitung von Lienhard und Lienhard [1] erklärt sind.
\frac {\partial^2 T}{\partial x^2} + \frac {\partial^2 T}{\partial y^2} + \frac {\partial^2 T}{\partial z^2} + \frac {\dot{q}}{k} = \frac {1}{\alpha}\frac{\partial T}{\partial t}Zur Berechnung von Wärmebrücken in Gebäuden werden die Materialien in aller Regel keine Wärme pro Volumeneinheit erzeugen. Der Term
\frac{\dot{q}}{k}fällt also heraus und im stationären Zustand, wenn sich alle Gebäudeteile auf eine Endtemperatur erwärmt haben, gilt:
\frac{\partial T}{\partial t} = 0Für Wärmebrücken reduziert sich damit die partielle Differentialgleichung der Wärmeflüsse auf:
(\frac {\partial^2 T}{\partial x^2} + \frac {\partial^2 T}{\partial y^2} + \frac {\partial^2 T}{\partial z^2})\space\alpha = 0Die Wärmeleitfähigkeit α ist nur dann vernachlässigbar, wenn sie in den Richtungen (x, y, z) gleich ist. In diesem Fall ergibt sich die Finite-Difference-Knotentemperatur als Durchschnitt der umgebenden Knoten[3]. Ansonsten besagt die PDE des stationären Zustands, dass sich die Wärmeströme aufheben und die Knotentemperaturen aus einem gewichteten Mittel folgen.
Wie beispielsweise bei Causon & Mingham[2] hergeleitet, approximieren sich die zweiten Ableitungen als:
\frac {\partial^2 T}{\partial x^2} (x_i) \approx \frac{T_{i+1} - 2T_i + T_{i-1}}{\Delta x^2}In der diskretisierten PDE gehen nun auch die diskretisierten Wärmeleitfähigkeiten zu beiden Seiten ein. Im Ergebnis erhält man eine Faktorisierung wie in Gleichung (2).
Quellenverzeichnis
[1] A Heat Transfer Textbook, 5th Edition, Lienhard and Lienhard
[2] Introductory Finite Difference Methods for PDEs, Causon & Mingham
[3] Mechanical Engineering Methods, Elliptic PDEs, Kyle Niemeyer
[4] The Analytical Theory of Heat. Dover Publications, Inc., New
York, 1955. Reprint of Fourier’s 1822 monograph.
